Nombre dérivé et tangente
Exercice 1 : Lecture graphique (Tangente)
La courbe \( C_f \) ci-dessous est la courbe représentative d'une fonction \( f \) dérivable sur \( \mathbb{R} \text{.} \)
La droite \( (\text{AB}) \) est tangente à la courbe \( C_f \) au point \( \text{A} \) d'abscisse \( 2 \text{.} \)
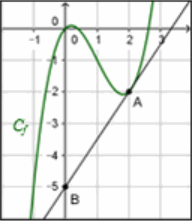
À l'aide du graphique, déterminer \( f(2) \) et \( f'(2) \text{.} \)
Exercice 2 : Lecture graphique (Nombres dérivés)
Voici la courbe représentative \( C_f \) d’une fonction \( f \) définie sur \( \mathbb{R} \text{.} \)
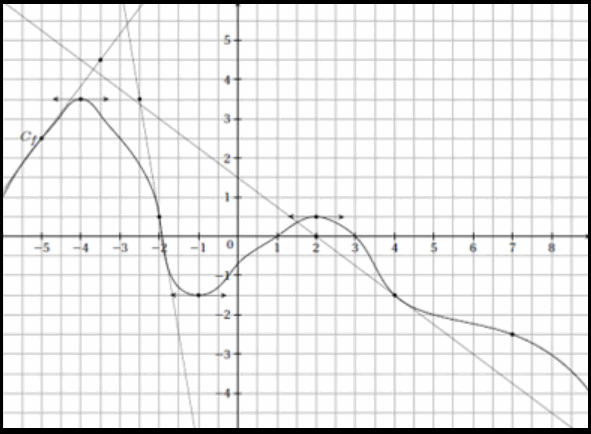
\( 1. \) Par lecture graphique, déterminer les valeurs de \( f'(-5) \text{,} f'(-4) \text{,} f'(-2) \) et \( f'(4) \text{.} \)
\( 2. \) Déterminer une équation de la tangente à \( C_f \) au point d’abscisse \( 4 \) et une équation de la tangente à \( C_f \) au point d’abscisse \( -2 \text{.} \)
Exercice 3 : Équation de tangente
On a représenté ci-dessous la courbe \( (C) \) représentative de la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = x^3 + 3x^2 - x - 2 \text{,} \) ainsi que le point \( A(1 ; 1) \text{.} \)
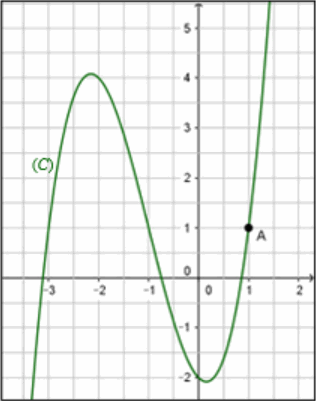
\( 1. \) Déterminer l'équation de la tangente \( (t) \) à \( (C) \) au point \( \text{A} \text{.} \)
\( 2. \) Tracer \( (t) \) sur le graphique ci-contre.
\( 3. \) Existe-t-il une autre tangente à \( (C) \) parallèle à \( (t) \) ? Justifier.
