Forme canonique d'un polynôme

Méthode 1 : Développer les formes canoniques

(1) $2(x-4)^2 + 3 = 2(x^2 - 8x + 16) + 3 = 2x^2 - 16x + 32 + 3 = $ $2x^2 - 16x + 35$ (D)

(2) $3(x+2)^2 + 1 = 3(x^2 + 4x + 4) + 1 = 3x^2 + 12x + 12 + 1 = $ $3x^2 + 12x + 13$ (B)

(3) $-(x-4)^2 + 2 = -(x^2 - 8x + 16) + 2 = -x^2 + 8x - 16 + 2 = $ $-x^2 + 8x - 14$ (A)

(4) $2(x - \frac{1}{2})^2 - \frac{1}{2} = 2(x^2 - x + \frac{1}{4}) - \frac{1}{2} = 2x^2 - 2x + \frac{1}{2} - \frac{1}{2} = $ $2x^2 - 2x$ (C)

---

Méthode 2 : Mettre les polynômes sous forme canonique

A: $-x^2 + 8x - 14 = -(x^2 - 8x) - 14 = -((x-4)^2 - 16) - 14 = -(x-4)^2 + 16 - 14 = $ $-(x-4)^2 + 2$ (3)

B: $3x^2 + 12x + 13 = 3(x^2 + 4x) + 13 = 3((x+2)^2 - 4) + 13 = 3(x+2)^2 - 12 + 13 = $ $3(x+2)^2 + 1$ (2)

C: $2x^2 - 2x = 2(x^2 - x) = 2((x-\frac{1}{2})^2 - \frac{1}{4}) = $ $2(x-\frac{1}{2})^2 - \frac{1}{2}$ (4)

D: $2x^2 - 16x + 35 = 2(x^2 - 8x) + 35 = 2((x-4)^2 - 16) + 35 = 2(x-4)^2 - 32 + 35 = $ $2(x-4)^2 + 3$ (1)

Pour $P_1(x) = -2x^2 + 4x + 16$ :

$P_1(x) = -2(x^2 - 2x) + 16$

$= -2((x-1)^2 - 1) + 16$

$= -2(x-1)^2 + 2 + 16$

$= $ $-2(x-1)^2 + 18$

---

Pour $P_2(x) = 3x^2 - 2x + \frac{4}{3}$ :

$P_2(x) = 3(x^2 - \frac{2}{3}x) + \frac{4}{3}$

$= 3((x-\frac{1}{3})^2 - \frac{1}{9}) + \frac{4}{3}$

$= 3(x-\frac{1}{3})^2 - \frac{3}{9} + \frac{4}{3}$

$= 3(x-\frac{1}{3})^2 - \frac{1}{3} + \frac{4}{3}$

$= $ $3(x-\frac{1}{3})^2 + 1$

1. Détermination de la forme canonique $f(x) = a(x - \alpha)^2 + \beta$

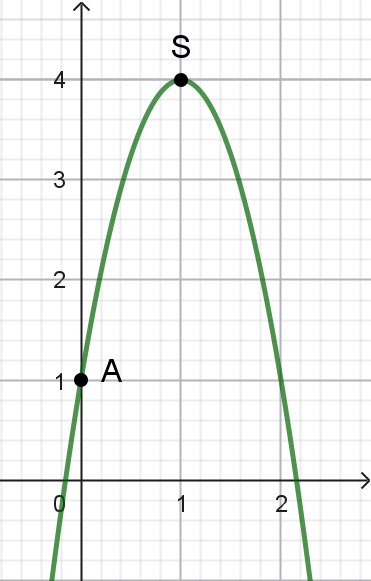
Par lecture graphique, on identifie les coordonnées du sommet $S(\alpha, \beta)$.
On lit : $\alpha = 1$ et $\beta = 4$.

L'équation de la parabole est donc de la forme $f(x) = a(x - 1)^2 + 4$.

Pour trouver le coefficient $a$, on utilise un autre point de la courbe, par exemple le point A(0, 1).
On remplace $x$ par 0 et $f(x)$ par 1 dans l'équation :
$f(0) = 1 \implies a(0 - 1)^2 + 4 = 1$
$a(-1)^2 + 4 = 1$
$a(1) + 4 = 1 \implies a = 1 - 4 \implies a = -3$.

La forme canonique de la fonction est $f(x) = -3(x - 1)^2 + 4$.

---

2. Détermination de la forme développée $f(x) = ax^2 + bx + c$

On développe la forme canonique trouvée :
$f(x) = -3(x - 1)^2 + 4$
$f(x) = -3(x^2 - 2x + 1) + 4$
$f(x) = -3x^2 + 6x - 3 + 4$
La forme développée est $f(x) = -3x^2 + 6x + 1$.

(On peut vérifier que $f(0) = -3(0)^2 + 6(0) + 1 = 1$, ce qui correspond bien au point A(0, 1).)

---

3. Détermination des racines

On cherche les valeurs de $x$ pour lesquelles $f(x) = 0$. On peut utiliser la forme canonique (plus rapide) ou la forme développée (avec le discriminant).

Méthode 1 (avec la forme canonique) :
$f(x) = 0 \implies -3(x - 1)^2 + 4 = 0$
$4 = 3(x - 1)^2$
$(x - 1)^2 = \frac{4}{3}$
On applique la racine carrée :
$x - 1 = \sqrt{\frac{4}{3}}$ ou $x - 1 = -\sqrt{\frac{4}{3}}$
$x - 1 = \frac{2}{\sqrt{3}}$ ou $x - 1 = -\frac{2}{\sqrt{3}}$
$x = 1 + \frac{2\sqrt{3}}{3}$ ou $x = 1 - \frac{2\sqrt{3}}{3}$.

Méthode 2 (avec la forme développée) :
$f(x) = -3x^2 + 6x + 1 = 0$. On calcule le discriminant $\Delta = b^2 - 4ac$.
$\Delta = (6)^2 - 4(-3)(1) = 36 + 12 = 48$.
$\sqrt{\Delta} = \sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}$.
Les deux racines sont :
$x_1 = \frac{-b - \sqrt{\Delta}}{2a} = \frac{-6 - 4\sqrt{3}}{2(-3)} = \frac{-6 - 4\sqrt{3}}{-6} = \frac{6 + 4\sqrt{3}}{6} = 1 + \frac{2\sqrt{3}}{3}$.
$x_2 = \frac{-b + \sqrt{\Delta}}{2a} = \frac{-6 + 4\sqrt{3}}{2(-3)} = \frac{-6 + 4\sqrt{3}}{-6} = \frac{6 - 4\sqrt{3}}{6} = 1 - \frac{2\sqrt{3}}{3}$.

Les racines du polynôme sont $x_1 = 1 - \frac{2\sqrt{3}}{3}$ et $x_2 = 1 + \frac{2\sqrt{3}}{3}$.

1. a) On développe la forme canonique :
$-0,2(x-2)^2 + 16,2 = -0,2(x^2 - 4x + 4) + 16,2 = -0,2x^2 + 0,8x - 0,8 + 16,2 = $ $-0,2x^2 + 0,8x + 15,4$.
L'égalité est démontrée.

1. b) On factorise à partir de la forme canonique :
$f(x) = -0,2[(x-2)^2 - \frac{16,2}{0,2}] = -0,2[(x-2)^2 - 81] = -0,2[(x-2) - 9][(x-2) + 9]$.
Donc, $f(x) = -0,2(x-11)(x+7)$.

2. a) La hauteur de la falaise est $f(0)$.
$f(0) = -0,2(0)^2 + 0,8(0) + 15,4 = 15,4$. La falaise mesure 15,4 m.

2. b) Le plongeur touche l'eau quand $f(x) = 0$.
$-0,2(x-11)(x+7) = 0$. Les solutions sont $x=11$ ou $x=-7$. Comme $x \ge 0$, le plongeur touche l'eau à 11 m de la falaise.

2. c) La hauteur maximale est donnée par le sommet de la parabole, via la forme canonique $f(x) = -0,2(x-2)^2 + 16,2$.
Le maximum est atteint pour $x=2$. La hauteur maximale est de 16,2 m.

1. Expression de l'aire $A(x)$

L'aire du triangle DMN est égale à l'aire du carré ABCD moins la somme des aires des trois triangles rectangles ADM, MBN et DCN.

Aire(ABCD) = $10 \times 10 = 100$ cm$^2$.

Aire(ADM) = $\frac{AD \times AM}{2} = \frac{10 \times x}{2} = 5x$.

Aire(MBN) = $\frac{MB \times BN}{2} = \frac{(10-x) \times x}{2} = \frac{10x - x^2}{2} = 5x - \frac{1}{2}x^2$.

Aire(DCN) = $\frac{DC \times CN}{2} = \frac{10 \times (10-x)}{2} = 5(10-x) = 50 - 5x$.

$A(x) = \text{Aire(ABCD)} - (\text{Aire(ADM)} + \text{Aire(MBN)} + \text{Aire(DCN)})$

$A(x) = 100 - (5x + 5x - \frac{1}{2}x^2 + 50 - 5x) = 100 - (5x - \frac{1}{2}x^2 + 50)$

$A(x) = 100 - 5x + \frac{1}{2}x^2 - 50 = \frac{1}{2}x^2 - 5x + 50$.

2. Forme canonique de $A(x)$

$A(x) = \frac{1}{2}(x^2 - 10x) + 50$

$= \frac{1}{2}((x-5)^2 - 25) + 50$

$= \frac{1}{2}(x-5)^2 - \frac{25}{2} + 50$

$= \frac{1}{2}(x-5)^2 - 12,5 + 50$

La forme canonique est $A(x) = \frac{1}{2}(x-5)^2 + 37,5$.

3. Aire minimale

La forme canonique de $A(x)$ est $a(x-\alpha)^2 + \beta$ avec $a=\frac{1}{2}$, $\alpha=5$ et $\beta=37,5$.

Comme $a > 0$, la fonction $A(x)$ admet un minimum pour $x=\alpha$.

L'aire est minimale pour $x = 5$ cm. Cette aire minimale est $A(5) = 37,5$ cm$^2$.