Géométrie : Les Angles du Triangle
Exercice 1 : Angles et Perpendiculaires
On considère la figure ci-contre :
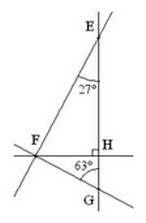
- En utilisant les informations données sur la figure ($\widehat{HEF} = 27^\circ$, $\widehat{EHF} = 90^\circ$, $\widehat{FHG} = 90^\circ$ et $\widehat{HGF} = 63^\circ$), calculer les mesures des angles $\widehat{EFH}$ et $\widehat{HFG}$.
- Prouver que les droites (EF) et (FG) sont perpendiculaires de 2 façons différentes.
Exercice 2 : Points Alignés et Parallèles
On considère la figure ci-dssous. En utilisant le codage et les informations suivantes :
- $\widehat{EAF} = 32^\circ$, $\widehat{AEF} = 58^\circ$, $\widehat{ABE} = 64^\circ$, $\widehat{EBC} = 68^\circ$, $\widehat{ECB} = 87^\circ$
- Codage : $BC = CD = DE$, $\widehat{CDE} = 90^\circ$ et $AE = BE$. (Note : le codage $AE=AF$ sur l'image est une erreur, on utilise $AE=BE$ et les valeurs d'angle du texte).
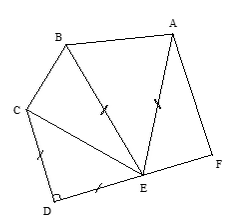
- Calculer les mesures d'angles nécessaires afin de déterminer si les points D, E et F sont alignés ou pas.
- Les droites (CD) et (AF) sont-elles parallèles ? Justifier.
Exercice 3 : Construction d'un Triangle Isocèle
Construire un triangle ABC isocèle en C tel que $AB = 6$ cm et $\widehat{BCA} = 50^\circ$.
Expliquer la méthode de construction.
Exercice 4 : Calculs d'angles et Alignement
On considère la figure ci-dessous avec les informations suivantes :
- $\widehat{HEL} = 40^\circ$, $\widehat{EHL} = 90^\circ$
- $\widehat{FLG} = 30^\circ$, $\widehat{LGF} = 80^\circ$
- Codage : $FH = FL$ (triangle HFL isocèle en F)
- Codage : $HL = LG$ (triangle HLG isocèle en L)
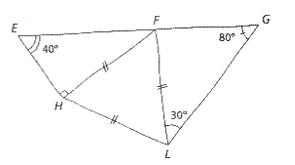
- En utilisant les informations portées sur la figure, calculer tous les angles de la figure (détailler les calculs pour chaque triangle).
- Les points E, F et G sont-ils alignés ? Justifier la réponse.
Exercice 5 : Triangle et Bissectrice
Soit un triangle ABC tel que $\widehat{BAC} = 44^\circ$ et $\widehat{ABC} = 72^\circ$.
- Calculer la mesure de l'angle $\widehat{BCA}$.
- La bissectrice de l'angle $\widehat{ABC}$ coupe le segment [AC] en un point D. Calculer la mesure de l'angle $\widehat{BDC}$.
